Dynamic Headroom Measurement

[VAR]

Much of the vintage gear that runs across my bench has a Dynamic Headroom specification. While the QA40x has an Amp Dynamics automated test which can provide useful information, it does not provide a Dynamic Headroom measurement. I thought I would share how I have been making this measurement- criticisms welcomed. Since a lot of the gear probably used the old IHF-A-202 definition for the Dynamic Headroom, that is what I have used (paragraph 3.2).

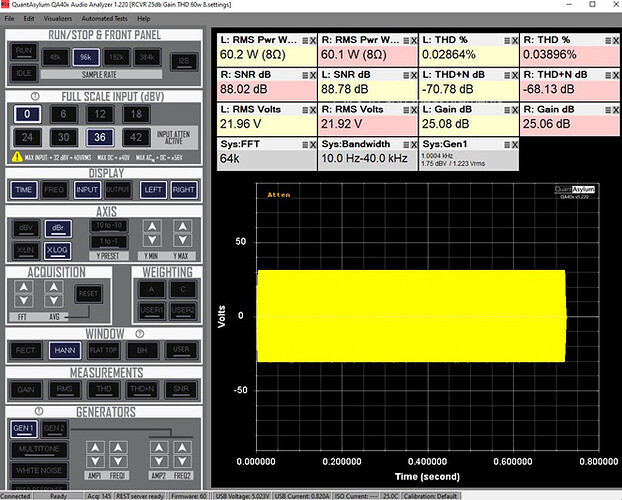
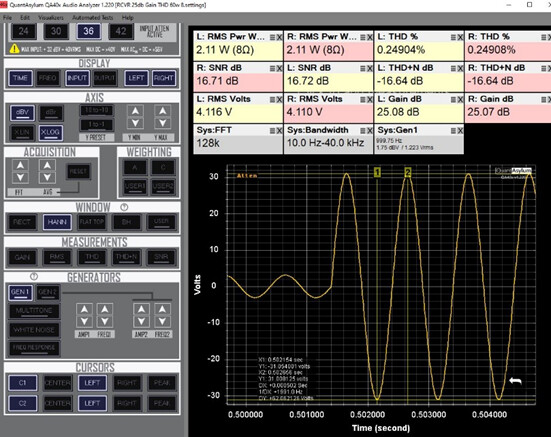
For this example, I am using a receiver that is rated for 60w/8ohms, so I started by setting it for that at 1khz- the response shown below:

I now switch the DISPLAY to TIME:

Next, I drag a “zoom window” around a small area of the beginning of the wave form and get this:

I turn the cursors on and put them at the min and max of the waveform:

The delta Y (62v) gives me the 1st voltage I enter into the spreadsheet for the Vpp for Pnom:

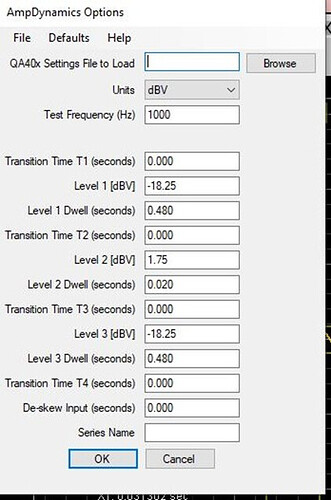
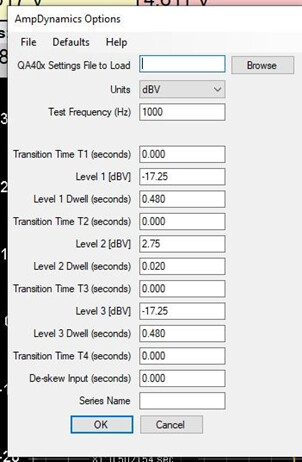
I will come back to the spreadsheet in a bit. I now select the AmpDynamics automated test and populate it with these settings, and run the test:

The resulting waveform will be something like this:

I then zoom in on the larger waveform at .5 sec and end up with something like:

There is no clipping of the waveform so I go back to the AmpDynamics automated test and increase the amplitude of input signal (note that 1.75dBV was the input level that yielded 60w) Levels 1 & 3 by 1dB (you can go more or less to start with, of course). You must also increase Level 2 by the same amount ( 1dB):

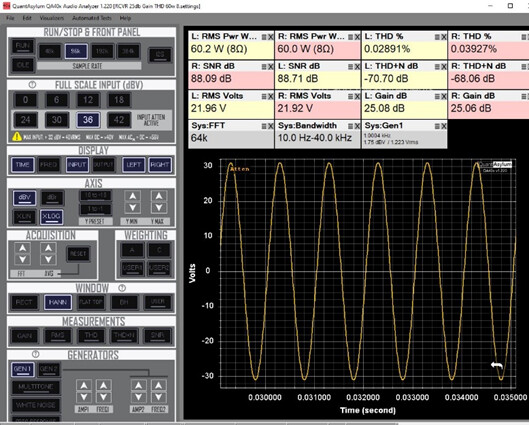
Press OK to run the test, repeating until you see some clipping of the waveform- remember to change the values of each such that levels 1 & 3 are the same and 20dB less than Level 2- eventually you will get a plot something like this that shows some clipping:

Placing the cursors at the maximum & minimum of the waveform gives a delta of 76.12V, which gets entered in the spreadsheet as the Vpp for Pmax:

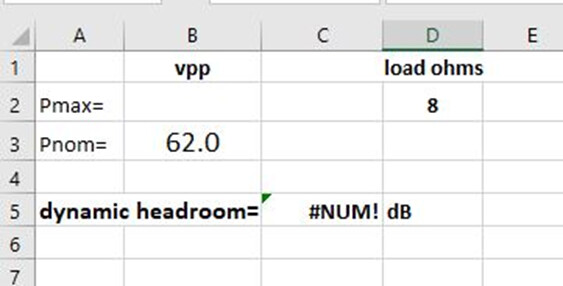
The dynamic headroom is then calculated to be 1.78dB, which was close to the spec. I will paste the equation below in case anyone wants to try this (and check my work):
=10*LOG10(((((B2/2)/1.414214)^2)/D2)/((((B3/2)/1.414214)^2)/D2))

[restorer-john]

This is all very good work Scott. I’ll have to have a go myself, as I found the dynamics plugin a bit awkward to use.

I’ve always done dynamic headroom manually as it is very fast, repeatable and doesn’t need an analyzer. A CD source playing a standard EIA (20mS@0dB/480mS@-20dB) or EIAJ/JIS (8mS@0dB/24mS@zero) toneburst for Japanese gear (they are different) and a scope. Only takes a few seconds to ramp up the volume/level until the bursted cycles get clipped and you back it off, read the value and calculate the power/headroom.

A DSO makes it even easier as you can have it trigger on the bursts and do the math for you.

I can email the standard .wav files I use if you want. They are off one of my test discs.

[VAR]

@restorer-john Thanks for your comments and yes I would like to try out your .wav file. The old IHF spec I referenced used 480ms and 0/-20dB. It would be nice if there was a Dynamic Headroom automated test that set the defaults up for the method you want- I am sure I mentioned that at some point in the forum. I am not sure I follow about how you would trigger the scope, but I like the idea of using the volume control. More stuff to play around with and learn about.