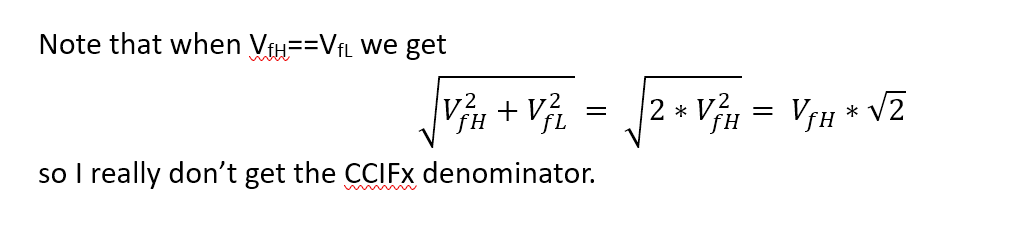QA40xPlot Thread

[captnaudio]

Hi Mark,

If you could already replicate the bugs I reported, I have little more to add.

Here is an example for “custom” with SMPTE conditions (gen1 = -2 dBV, 60 Hz; gen2 = 7 kHz, -14 dB) the plot does not run (does not start).
Further, it “hangs” (crashes), meaning this: it doesn’t do anything, if I click on “Stop” it does not react .

You said:…“pretty tough to explain to customers how this is all right when you have three different formulas for IMD”
I understand. However, if you don’t have three different formulas then the results get wrong. No way to avoid it.

I didn’t check yet, if AES-17 and TDFD phono have other specific math behind. I think you could trust REW for the purpose of running a comparative test for these.

[captnaudio]

I don’t have access to the original AES standards applicable to the measurements AES-17 DFD and AES-17 MD. From the results reported in REW with these methods, I am deducing the following:

1. AES-17 DFD
f1 = 18 kHz, f2 = 20 kHz; 1:1 amplitude ratio
reference frequency is f1 (or f2) only.

IMD (AES DFD) = V(f2-f1) / V(f1)
Calculation is is identical to CCIF2.
Other IM products than V(f2-f1) can be neglected in most cases.

If higher IM products are not neglected, general formula:
Quote from REW: “The AES17 DFD IMDAES figure is based on the levels at f2 - f1 (2 kHz), 2f1 - f2 (16 kHz) and 2f2 - f1 (22 kHz), the reference level for the IMDAES percentage figure is the level at f1 (18 kHz).”
IMD (AES DFD) = sqrt[V(f2-f1)^2 + V(2f1 - f2)^2 + V(2f2 - f1)^2] / V(f1)

2. AES-17 MD
f1 = 41 Hz, f2 = 7993 Hz, 4:1 amplitude ratio
reference frequency is f2 only (7993 kHz).

Quote REW:
"The AES17 MD IMDAES is calculated from the rms sum of the 2nd order (d2) components, the reference level for the percentage figure is the level at f2. "

IMD(AES MD) = sqrt [V(f2-f1)^2 + V(f2+f1)^2] / V(f2)

3. TDFD phono
f1 = 3005 Hz, f2 = 4462 Hz, 1:1 amplitude ratio
reference amplitude is is V(f1) + V(f2) (like in power method)

Quote REW:
“For TDFD Phono and TDFD akl d2L (f2 - f1) and d3L (2*f1 - f2) are used.”
IMD(TDFD phono) = sqrt [V(f2-f1)^2 + V(2f1-f2)^2] / sqrt [V(f1)^2 + V(f2)^2]

Regards
Reinhard

[MarkZ]

It looks like Virtins changed their minds in 2024 and went from this value to the linear addition I assume based on CCIF specifications. Rather bizarre specification since the sum of the two fundamentals has no physical meaning at all.

Anyway, I should have this all buttoned up in a day or two.

[captnaudio]

Hi Mark,

Sorry for the trouble, my mistake. My apologies!
Of course, you are right.

The denominator in CCIF is the arithmetic sum Vf1 + Vf2 and not the geometric sum sqrt [Vf1)^2 + V(f2)^2]. Virtins corrected it in 2024 as they did also for the SMPTE / DIN formula.
As you write, the arithmetic sum Vf1 +Vf1 in CCIF has no plausible physical meaning, considering that both voltages are uncorrelated (in phase). Nevertheless, its defined that way by CCIF.
For that reason, IMD by CCIF method (denominator = 2 V(f1) results in a 6 dB higher number than the DFD method (denominator = V(f1) only).

Audio Precision’s note / explanation (for measurements with their audio analyzers):

“For analysis DFD selectively measures the 2nd and 3rd order intermodulation products, combines their values arithmetically and provides a result that is the ratio of the sum of the products to a reference voltage defined as 2x the voltage of f2 (effectively, the sum of f1 and f2)… DFD measurements are made in the same way as CCIF measurements, differing only in amplitude calibration. DFD results are expressed as values 6.02 dB lower than CCIF.”

and

“For analysis CCIF selectively measures the 2nd and 3rd order intermodulation products, combines their values arithmetically and provides a result that is the ratio of the sum of the products to a reference voltage defined as 2x the voltage of f2 (effectively, the sum of f1 and f2)…CCIF measurements are made in the same way as DFD measurements, differing only in amplitude calibration. CCIF results are expressed as values 6.02 dB higher than DFD.”

Regards
Reinhard

[captnaudio]

I have set up an old amplifier for measurement which has high IMD. With that one it is easy to compare different software (QA40xPlot, REW, ARTA) while the hardware remains the same.

I know, that a comparison at this point is premature. Perhaps it can help to spot the differences in the formulas to get it right. Its difficult enough because of the definitions lack the required precision in many documents. And no guarantee, That REW is always right here.

Currently (9 pm CET, Berlin) my results are these:

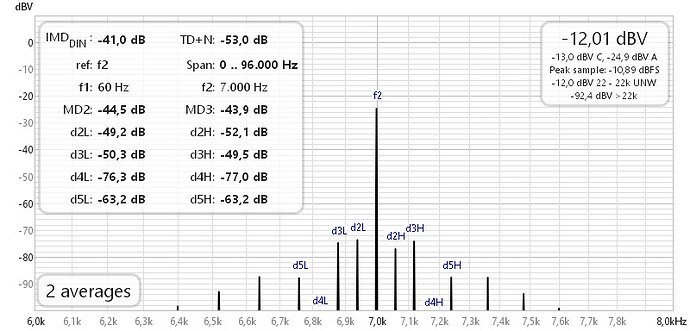
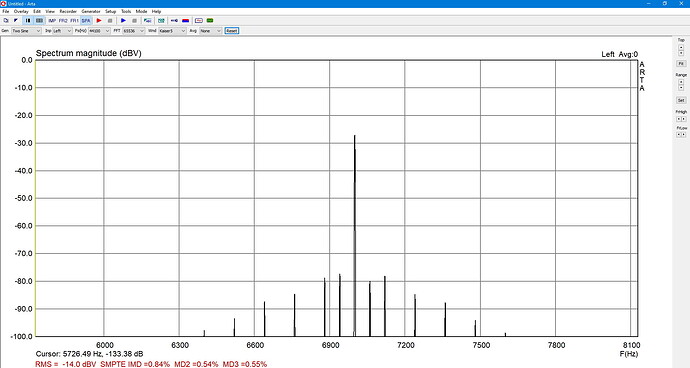
1. SMPTE 60 Hz +7 kHz 4:1
QA40xPlot and REW as well as ARTA: Same result within 1 dB.

a) QA40xPlot

b) REW

c) ARTA IMD = 0,84 % = -41,5 dB

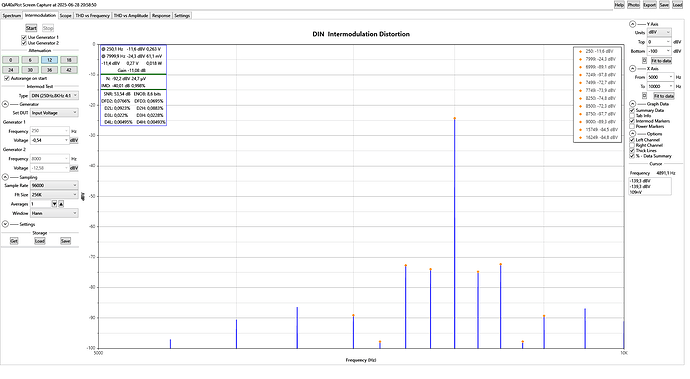
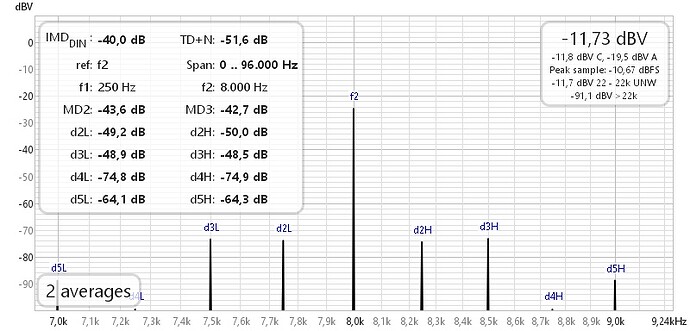
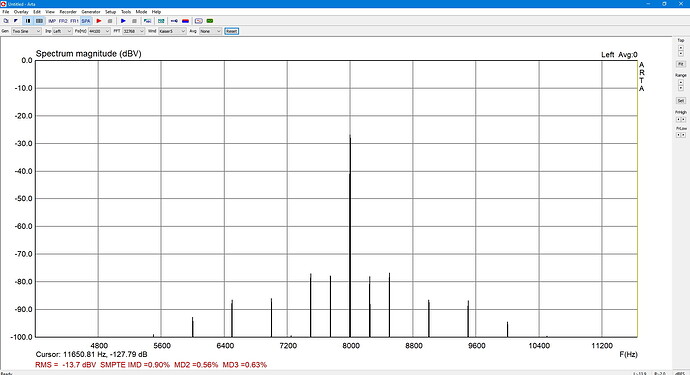
2. DIN 250 Hz +8 kHz 4:1
QA40xPlot and REW as well as ARTA: Same result within 1 dB.

a) QA40xPlot

b) REW

c) ARTA
DIN IMD = 0,90 % = -41 dB

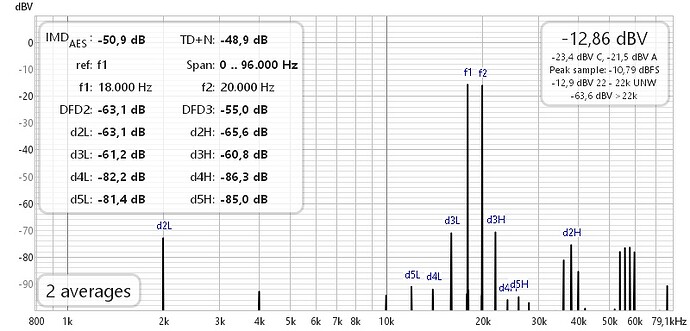
3. CCIF 19 kHz + 20 kHz 1:1
QA40xPlot and REW as well as ARTA almost same result (2 dB difference)
However, in QA40xPlot the total voltage in summary window cannot be right, shown there as -14,6 dBV, although f1 (19 kHz) and f2 (20 kHz) are each at -15,3 dB. Total voltage shall be at least being indicated as -12,3 dB.

a) QA40xPlot

b) REW

c) ARTA IMD = 0,23 % = -52,8 dB

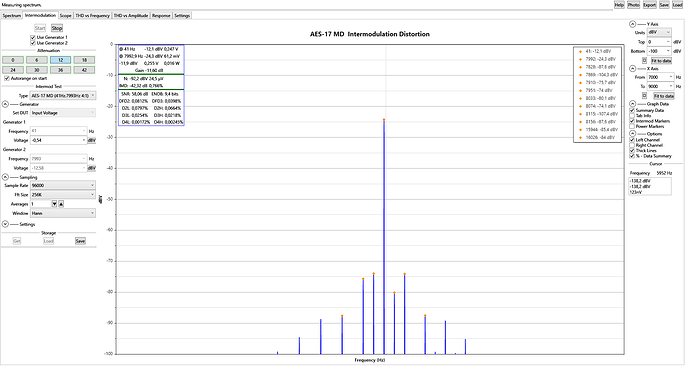
4. AES-17 MD 41 Hz +7993 Hz 4:1
QA40xPlot and REW differ by 6 dB. ARTA (using SMPTE method) is close to QA40xPlot.

Because the SMPTE/DIN method is using arithmetic summing for the components belonging to the same order, before rms summing all orders that makes the SMPTE result 3 db larger than the AES method.
Where the other remaining 3 dB difference is coming from, no idea.

a) QA40xPlot

b) REW

c) ARTA IMD 0,85 % = -41,4 dB

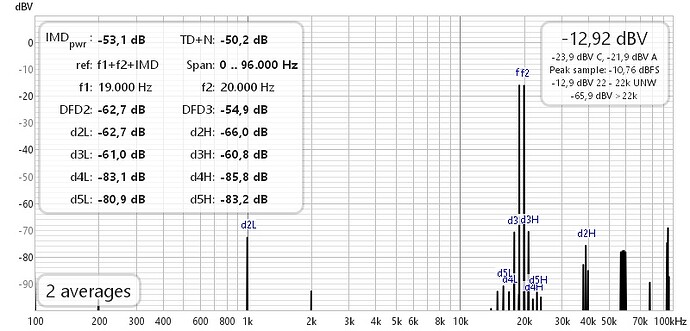
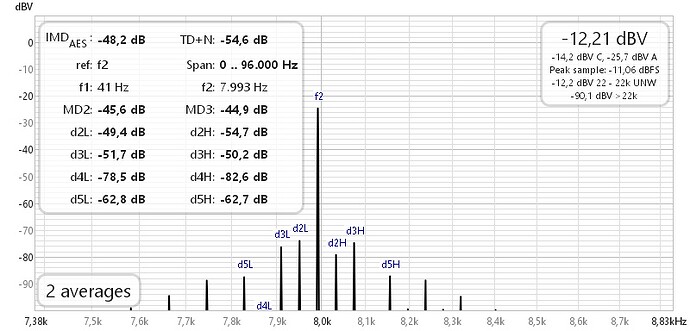
5. AES-17 DFD 18 kHz + 20 kHz 1:1
QA40xPlot and REW differ by 3 dB. ARTA, using the CCIF method, is close to QA40xPlot.

a) QA40xPlot

b) REW

c) ARTA IMD = 0,22% = -52,8 dB

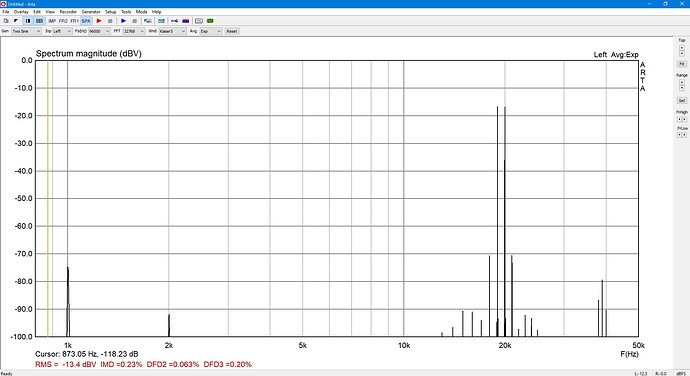
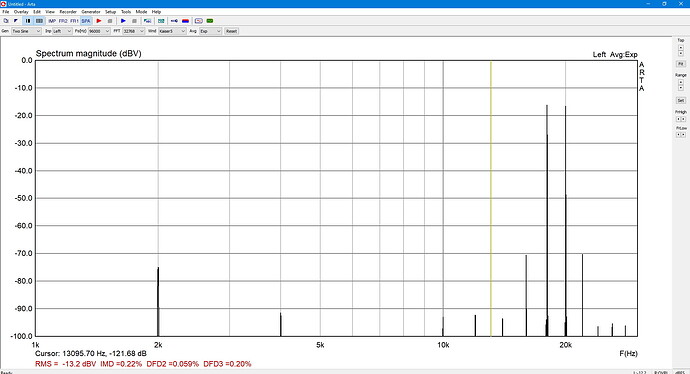
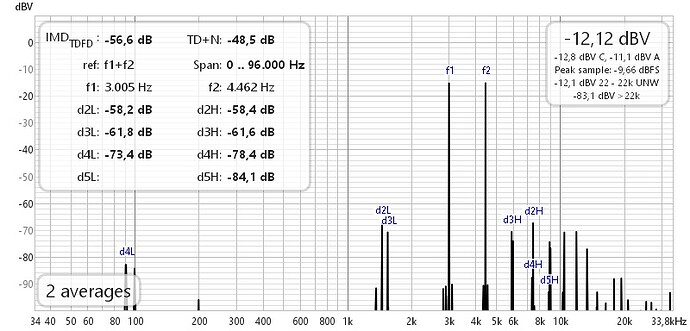
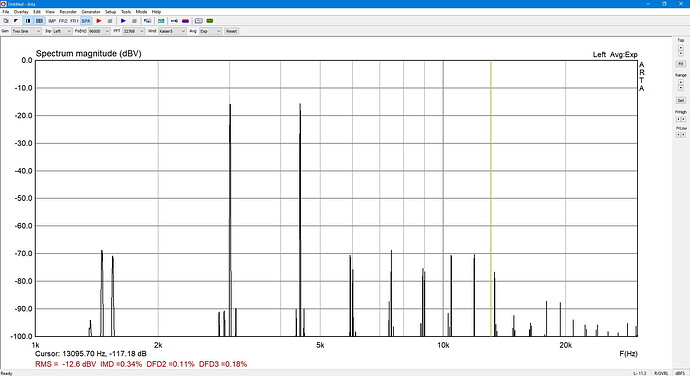
6. TDFD phono 3005 Hz + 4462 Hz 1:1
QA40xPlot and REW are by 11 dB apart.
ARTA, using the CCIF method, is 3 dB from QA40xPlot.

If I do the math manually according to the formula quoted above in REW, but with the arithmetic sum for f1 and f2 in the denominator rather than the rms sum, I arrive for the QA40xPlot data at -57 dB, same as reported by REW. Seems to me that the formula in this case applied by REW is

IMD(TDFD phono) = sqrt [V(f2-f1)^2 + V(2f1-f2)^2] / (V(f1) + V(f2))
(like CCIF) and not the one I assumed above with the rms sum in the denominator.

Like wise, the math with the data from ARTA arrives at -58 dB then.

a) QA40xPlot

b) REW

c) ARTA IMD = 0,34 % = -49 dB

Regards
Reinhard

[napedersen]

Measuring on an amplifier.
Using the Spectrum tab, and choosing Watts as Y Axis unit , the application says Not responding, and needs to be shut down.

Regards
Niels

Regards

[MarkZ]

Hi @napedersen ,

Could you check your amplifier load setting for me? When I set it to 0 I don’t crash but maybe you do? I can’t replicate this - I would suggest checking the load value and if it’s not zero maybe get rid of your QADefault.cfg in documents if you have one and try again since it could be some leftover value.

If it continues to crash after removing qadefault and checking load then please post a photo of the screen so I can see your settings.

Thanks,

Mark

[MarkZ]

hi @captnaudio

well, I’ve posted a new build for you to take a look at. Thanks for all the help so far. This build should be correctly calculating IMDs. I’m using the ratio > 2 or ratio > 7 ARTA-style calculation.

You can easily validate the math if you care to because if you look at the summary box I’ve relabeled the individual distortion components. Turn off the “% - Data Summary” checkbox and it will show absolute voltage values.

d2L = fH-fL
d2H = fH+fL
// the below are shown backwards on the table (oops) I’ll fix that but for now it shows
d3L = fH + 2fL
d3H = fH - 2fL
d3La = fL + 2fH
d3Ha = fL - 2fH
d4L = fH + 3fL
d4H = fH - 3fL

any frequencies out of range show an IMD value of 0

[VAR]

@MarkZ - Is it possible to move the summary tables around to different positions on the graph where “nothing may be going on” ? Thanks for all your efforts.

[MarkZ]

I would like to do that. I investigated moving the windows two weeks ago and it was way more work than I’d hoped so I stuck it in my procrastinate list and made them translucent :). I’ll look at it again now that my math stuff is nearly done finally.

Mark

[VAR]

@MarkZ- It would be nice to be able to drag them around to another part of the screen, but I have no idea how involved that is with programming and apparently not a lot of requests for that feature. One could have the Right Ch window more towards the upper right side of the graph where not much is typically going on in my experience. Thanks for investing

[restorer-john]

@MarkZ Would it be difficult to add a L/R/L+R option for the generators so we can choose what we send to each channel? That would open the door to other tests for free, like channel separation vs frequency etc. Even just spot crosstalk tests, where you could send two different frequency sines to each channel and look at the crosstalk in the opposite FFT.

[MarkZ]

It’s trivial to send a different signal to the right channel. I’ve almost done it a few times but never really had an application for it other than crosstalk and then it’s mainly extra gui that most people won’t have a use for.

I would personally like a Crosstalk test, however, which puts it way up on the list.

[cfortner]

Another thing: Your software doesn’t save the windows position, would it be complicated to add this?

Thanks a lot for your great work!

[MarkZ]

Hi,
It does save the current window. If you use save configuration on exit then when you restart the program it will bring it up in the current window.

Mark

[captnaudio]

Hi Mark,

Comparing QA40xPlot with REW and ARTA, I get the same results (within 1 dB) now for:

DIN (250 Hz : 8 kHz, 4:1)
SMPTE (60 Hz : 7 kHz, 4:1)
AES-17 DFD (18 kHz : 20 kHz, 1:1)

However, I see different results for
AES-17 MD (41 Hz : 7993 Hz, 4:1)
REW is by 6 dB lower than QA40xPlot as observed before (In my test example QA40xPlot -47 dB vs. REW -53 dB).
ARTA is close to QA40xPlot within 1 dB.
Obviously, REW is using a different formula here..

TDFDphono (3005 Hz : 4462 Hz, 1:1)
REW IMD is 2 dB lower than QA40xPlot.
In my test example QA40xPlot -64 dB vs. REW -66 dB.
ARTA is reporting 6 dB higher IM distortion than QA40xPlot this time.
I am going to check on these differences more closely.

I am not saying that REW is right. Could be a flaw in the calc. done by REW. Need to check more closely.

Regards
Reinhard

[MarkZ]

Thanks, I’ll take a look at these values and see what’s happening.

I have an update today or tomorrow to post that fixes the table labels and lets you move data summary boxes on-screen.

After that, it’s summer and my schedule for the next 6 weeks or so is very busy and updates will be rare until fall.

Mark

[cfortner]

Hi Matt,

unfortunately it doesn’t remember the window position (I need it maximized).

Opened and window made a little larger, but not maximised

Window maximized

Program closed and window position after reopening

Edit: Actual Windows 11

[MarkZ]

Hi,

Yes, I don’t support maximized or minimized at this time. For now, I’d recommend you drag the window so it nearly fills the screen. Max/min status is kind of weird to trap so I didn’t for now.

Mark

[cfortner]

Ok, thanks, that’s a workaround, I’ll open it nearly maximized.